2022年社区工作者考试模拟题—行测（2.17）（2）

2022-02-17 09:25:26 来源: 中公社区工作者考试网

参考答案与解析

1.【答案】C。中公解析：方法一，根据小张不去甲户，小李不去丙户分类，共分三类，①小张去乙户，小李去甲户，则小张、小李分别去的两户还需各安排1名干部，剩余的2名干部去丙户，有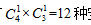安排方式;②小张、小李均去乙户，则剩下两户每户安排2人，有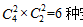安排方式;③小张去丙户，小李可以去甲或乙户，有2种选择，此时再安排其余人，安排方式同①有12种，故当小张去丙户时，有2×12=24种安排方式。综上，分类相加，不同的安排方式有12+6+24=42种。

方法二，不考虑小张、小李的要求，总的安排方式有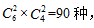小张去甲户的安排方式有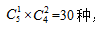，同理，小李去丙户的安排方式有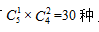，小张去甲户且小李去丙户的安排方式有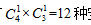。综上，符合条件的安排方式共有90-30-30+12=42种。

2.【答案】A。中公解析：10名运动员共要赛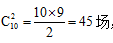，每场最少打2局，故比赛局数不少于45×2=90局。所有各局比赛最高比分为25∶23，则每局所有可能的得分情况为25∶23、24∶22、……、13∶11、12∶10和11∶9、11∶8、……、11∶1、11∶0，共24种。90÷24=3……18，故所求为3+1=4局。

3.【答案】B。中公解析：方法一，设工作总量为1，甲、乙单独工作时的效率分别为x和y，根据题干描述的工作情况可得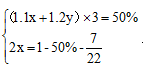，下式化简得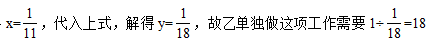小时。

方法二，甲单独做2小时完成全部工作的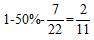，则甲单独完成这项工作需要11小时，根据“合作时甲的工作效率比单独做提高10%”可知，合作时和单独做时甲的工作效率之比为11∶10，同样的工作量，合作和单独做时甲用的时间之比为10∶11，因此按照合作的效率甲完成这项工作需要10小时，又知甲、乙合作6小时可完成工作，对比发现，甲4小时的工作量乙需要6小时，则甲6小时的工作量，乙需要9小时，因此按照合作的效率乙完成这项工作需要6+9=15小时，则乙单独做这项工作需要15×(1+20%)=18小时。